基本情報処理試験や応用情報処理試験などの情報処理試験で2進数の少数の問題が出題されたとき、意味が分からずいつも飛ばしていませんか?
私も情報処理試験に挑戦し始めたころ、2進数の少数の問題は意味が分からずいつも飛ばして、結果合格点に届かないなんてことがたびたびありました。
しかし、解けないままにしているのは非常にもったいないです。
2進数の仕組みを理解しておくことはエンジニアとしても重要な要素ですし、何よりコツさえつかんでしまえば2進数の少数はとても簡単な仕組みです。
私はこれまでに「基本情報技術者試験」「応用情報技術者試験」「プロジェクトマネージャ試験」に合格してきた現役エンジニアです。
私自身も2進数の少数を理解するのに苦労しました。
実際に私が試験勉強をする中で見つけてきた理解するコツもあわせてご紹介します。
「暗記」ではなく「理解」をして、2進数の少数の問題を得点源にできるように、マスターしていきましょう!
2進数の少数とは?
コンピュータはすべての情報を「0」と「1」で表現して動作しています。それは少数でも同じです。ですが実はコンピュータは少数の計算が得意ではありません。
整数部分の扱いについては下記の記事で解説しています。
ぜひとも併せて読んでみてください。
少数の場合、2進数では、小数点以下も「2の負のべき乗」で表現します。
例えば2進数の「0.1」は10進数では「0.5」となります。
それは少数点以下の値を2進数では以下のように表現するからです。
少数点第1位は 2^-1= 1/2 =0.5
少数点第2位は 2^-2= 1/4 =0.25
少数点第3位は 2^-3= 1/8 =0.125
少数点第4位は 2^-4= 1/16 =0.0625
少数点第5位は 2^-5= 1/32 =0.03125
なので2進数の「0.1」は「0.5」
2進数の「0.11」は「0.5+0.25=0.75」となります。
10進数から2進数への変換
では10進数の「0.6875」を2進数に変換してみます。
10進数の少数を2進数に変換は以下の手順で行います。
1)小数部分に2をかける
2)整数部分をメモしておき、整数部分が1であれば0にしてまた2をかける
3)1)、2)を小数部分が0になるまで繰り返す
図に表すと下記のようになります。
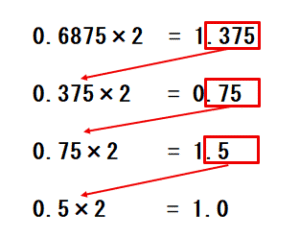
この計算結果の整数部分を小数点以下に並べることで2進数に変換することができます。
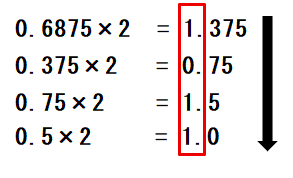
「0.1011」が10進数の「0.6875」を2進数に変換した値になります。
「0.1011」を10進数に変換してみて確認もしておきましょう。
少数点第1位は 2^-1= 1/2 =0.5
少数点第2位は 2^-2= 1/4 =0.25
少数点第3位は 2^-3= 1/8 =0.125
少数点第4位は 2^-4= 1/16 =0.0625
ですので、
1×0.5 + 0×0.25 + 1×0.125 + 1× 0.0625
=0.5+0.125+0.0625
=0.6875
となりますので正しく変換できてますね。
2進数の無限小数
では10進数の「0.1」を2進数に変換するとどうなるでしょう?
10進数から2進数へ変換する計算の手順にそって計算してみましょう。
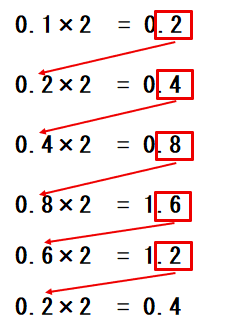
左辺の部分に0.2が2回出てきています。続きの計算をしても小数部分が0になることはありません。
10進数の「0.1」は2進数に変換すると「0.0001100110011・・・・」と無限に続く無限小数となります。
これはどうゆうことかというと10進数の「0.1」をコンピュータ上は正確には表現できないということです。
少数の誤差はなぜ起きる?
10進数の「0.1」は2進数に変換すると「0.0001100110011・・・・」と無限に続く、無限小数となる説明はしましたが、コンピュータで扱う情報量は無限ではありません。
決まったルールに従って、情報を四捨五入したり、切り上げたり、切り捨てて値を表現するようにしています。その結果、小数を使った計算にはどうしても誤差が生じてしまいます。
簡単な例でまずは実際に計算の誤差がどのように出るかを見てみましょう。
C#で書いたソースコードです。
doubleという浮動小数点の数値型の変数「x」と「y」を宣言し、
「x」には0.1 + 0.2の計算結果を代入、
「y」には0.3をそのまま代入しています。
そのあと「x」と「y」の値を比較し、
一致していれば「TURE」、一致していなければ「FALSE」をメッセージを
表示するようにしています。
0.1 + 0.2=0.3なので「x」と「y」どちらにも「0.3」が代入されているので
値は一致するはずです。
double x = 0.1 + 0.2;
double y = 0.3;
if (x == y)
{
MessageBox.Show("TRUE");//*********①
}
else
{MessageBox.Show("FALSE");//*********②
}
では実際に動作させたときのメッセージボックスを見てみましょう。
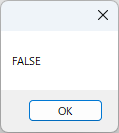
このように「FALSE」と表示されてコンピュータ上は一致しないと判断されます。
次はdoubleという浮動小数点の数値型の変数「sum」に対して0.1を1000回足す処理の計算結果をメッセージで表示する処理です。
行ってみます。
0.1を1000回足すので結果は100になるはずです。
double sum = 0.0;
for (int i = 0; i < 1000; i++)
{
sum += 0.1;
}
Console.WriteLine(sum);
MessageBox.Show(sum.ToString());
こちらも計算結果を見てみましょう。
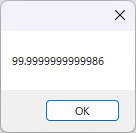
このように「100」とは表示されず「99.9999999999986」と表示されます。
誤差の種類
基本情報処理試験や応用情報処理試験などの情報処理試験では「情報落ち誤差」「丸め誤差」「桁落ち誤差」「打ち切り誤差」の4つが出題されます。
どんな計算をすると誤差が出てしまうのか、仕組みを理解しておくことで実務にも活かすことができるのでしっかりとそれぞれの誤差の特徴を掴んでおきましょう。
情報落ち誤差
非常に小さい数と非常に大きい数の足し算をしたときに、小さい値が無視されてしまう現象です。
丸め誤差
浮動小数点数では、有効桁数に限りがあります。
例えば「0.1」などの 正確に表せない値無限小数のため、ある程度のところで桁を丸めて近似値で表現します。
そのために発生する誤差です。
桁落ち誤差
ほぼ同じ大きさの数を引き算したときに、有効な桁が失われてしまう現象です。
打ち切り誤差
無限に続く計算を、途中で打ち切ることで生じる誤差です。
例えば円周率は10進数の無限小数です。円周率を「3.14」として計算することは多いと思いますが
まとめ
・2進数の少数は2^-n(べき乗)で表現する
・2進数の少数は2^-n(べき乗)で表現するため正確に表現できるのは2^-nの
組み合わせの値だけ
・2^-nの組み合わせ以外の少数は「無限小数」となるため近似値で表現する
・2^-nの組み合わせ以外の少数の計算は誤差が発生する
・誤差の種類は「情報落ち誤差」「丸め誤差」「打ち切り誤差」「桁落ち誤差」の4つ
です。2進数の少数をマスターして情報処理試験での得点源にしていきましょう!





